Nonlinear flow states and turbulence produced by helical magnetorotational-type instabilities (Solar Studies)

Project overview

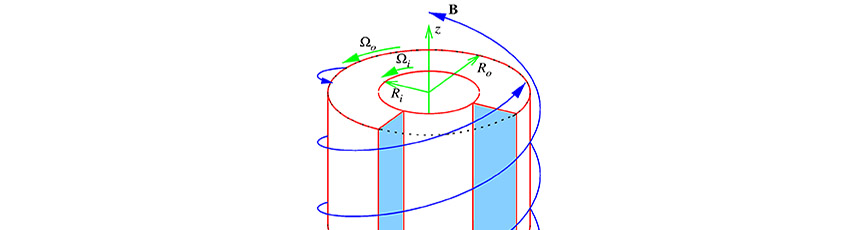
To investigate the origin of turbulence in hydrodynamically stable astrophysical flows by developing a nonlinear stability theory of helical magnetorotational instability (HMRI) and carrying out a systematic numerical analysis and modelling of finite-amplitude HMRI states which may affect the dynamics of the equatorial parts of the solar tachocline and dynamo action there.

Project objectives

The intention of the project is to develop a comprehensive nonlinear theory of helical magnetorotational instability (HMRI) and to carry out a systematic numerical analysis and modelling of finiteamplitude HMRI states which can explain the origin of turbulence in hydrodynamically stable astrophysical flows not affected by standard magnetorotational instability (SMRI). As with SMRI (Kagan & Wheeler, 2014) and Tayler instability (TI) (Rogers, 2011), HMRI is thought to be important for the dynamo action in the solar tachocline – a thin transition region with a thickness of ⇡ 0.04R separating the rigidly rotating radiative zone of outer radius 0.7R from the convective zone which rotates faster at the equator and slower at the poles (Spiegel & Zahn, 1992). The rotation rate increasing radially outwards in the equatorial part of the tachocline suppresses the SMRI but not the HMRI which can still be effective in this dynamically important solar region (Mamatsashvili et al., 2019). However, unlike the SMRI, the HMRI, according to the underlying linear stability theory, is limited to relatively slow rotational flows (Liu et al., 2006; Kirillov et al., 2012). The ability of the HMRI to destabilize highly inertial flows outside its linear instability range is unclear. Solving this theoretically challenging and astrophysically important problem is the main aim of this project.